「国語力」のすごさ
数学
|
[平成22年東京都立高校入試・数学・1] |
この問題を解くには、
国語の読解力と論理的思考力が必要不可欠です!
[求める解答]:「bがaの倍数となる目の出方」
→「倍数」=「ある整数の何倍かの数」
→bがaの倍数であるとき、整数bは整数aで割りきれる
※ 「倍数」という言葉の意味に注目すれば、
「1回投げて出た、小さいさいころの目bが、大きいさいころの出た目aで割りきれる組み合わせ」を求めればいいとすぐわかる
→bが1のとき、割りきれるaは1の1通り
→bが2のとき、割りきれるaは1と2の2通り
→bが3のとき、割りきれるaは1と3の2通り
→bが4のとき、割りきれるaは1と2と4の3通り
→bが5のとき、割りきれるaは1と5の2通り
→bが6のとき、割りきれるaは1と2と3と6の4通り
⇒正解は、1+2+2+3+2+4=「14通り」
[正解] 14通り
information
論理と情熱の国語(ジーワンラーニング中野駅前校)
〒164-0001
東京都中野区中野5-32-6
城西ビル202
電話 03-5942-5531
FAX 03-5942-5598
メール info@g-one.extrem.ne.jp
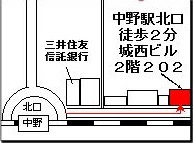
Google地図はこちらから
[開講場所]
ジーワンラーニング